Time Complexity
Time complexities are a way to measure how long a program takes to run. They are written like O(n) (pronounced "O of n").
But what do they actually mean?
You can think of time complexities as each operation taking n length of time, which scales with the size of your input.
For example, adding two numbers is a constant time operation (O(1), or "O of 1"). This means that no matter the size of your numbers (input), adding them (the operation) will always take the same amount of time.
For example, imagine 1 + 1 takes 100 nanoseconds. 25938 + 30292 will also take 100 nanoseconds, because the time taken to add two numbers is constant.
A linear search algorithm has a linear time complexity (O(n)). This is because in the worst case scenario, it has to iterate through every element in the array, and time complexities are measured by worst case performance.
Common Time Complexities and their Visualizations
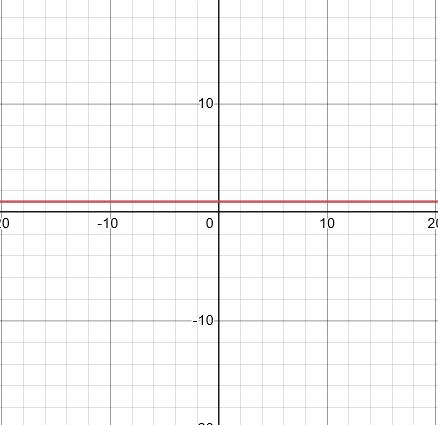
O(1), or constant time (usually found in array access or arithmetic operations):
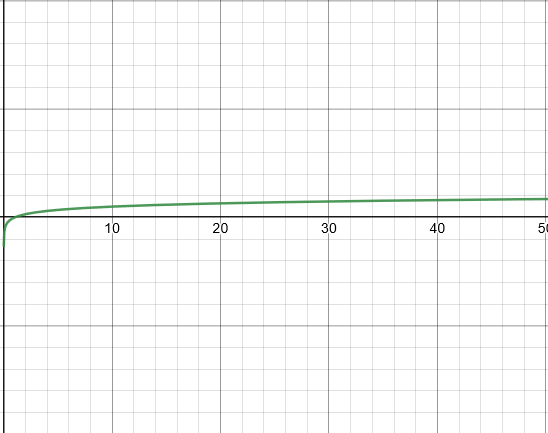
O(log n), or logarithmic time (binary search):
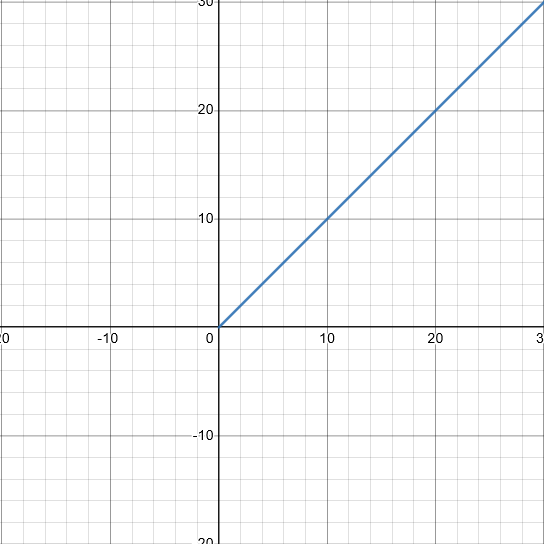
O(n), or linear time (linear search):
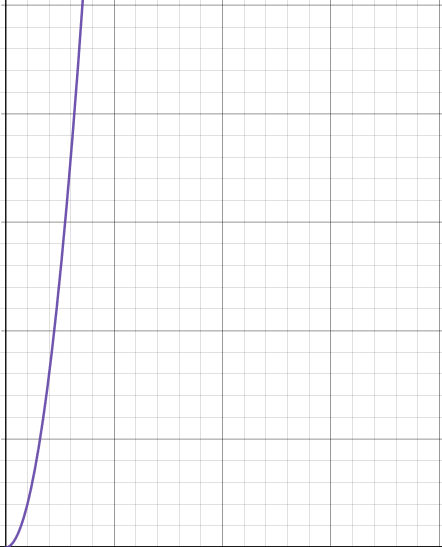
O(n log n), or quasilinear time (sorting algorithms):
O(n2), or quadratic time (linear search in a linear search):